Rangkuman setengah semester

Rangkuman

Link List

Link list adalah struktur data yang paling dasar.  Struktur data ini  dikenal juga dengan sebutan senarai berantai adalah struktur data yang terdiri dari urutan record data dimana setiap record memiliki field yang menyimpan alamat/referensi dari record selanjutnya (dalam urutan). Elemen data yang dihubungkan dengan link pada Linked List disebut Node. Biasanya didalam suatu linked list, terdapat istilah head dan tail. Head adalah elemen yang berada pada posisi pertama dalam suatu linked list.  Tail adalah elemen yang berada pada posisi terakhir dalam suatu linked list.  Link list juga disebut array dinamik.

Beberapa macam link list:

• Single linked list
• Double linked list
• Circular linked list

Single Link List

Single Linked List merupakan suatu linked list yang hanya memiliki satu variabel pointer saja. Dimana pointer tersebut menunjuk ke node selanjutnya. Biasanya field pada tail menunjuk ke NULL.

Double Link List

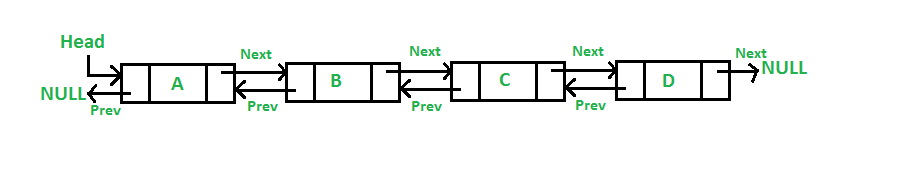
Double Linked List merupakan suatu linked list yang memiliki dua variabel pointer yaitu pointer yang menunjuk ke node selanjutnya dan pointer yang menunjuk ke node sebelumnya. Setiap head dan tailnya juga menunjuk ke NULL.

Circular Link List

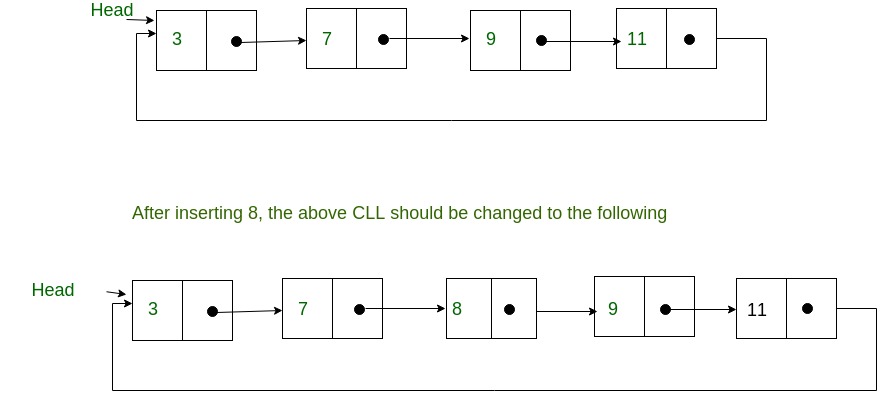
Circular Linked List merupakan suatu linked list dimana tail (node terakhir) menunjuk ke head (node pertama). Jadi tidak ada pointer yang menunjuk NULL

Stack

Stack adalah data struktur yang menyusun data secara berurutan.  Stack merupakan data struktur linear yang menggunakan prinsip LIFO (Last in First Out) yang berarti datang terakhir, keluar pertama. Stack dapat diimplementasikan menggunakan array ataupun linked list, masing-masing memiliki keutungan dan kelemahan masing-masing.  Menggunakan array akan lebih gampang karena array mereserve memory yang diperlukan lebih dahulu tetapi karena hal itu array tidak bisa fleksibel jika tiba-tiba kita perlu menambah elemen baru pada saat kapasitas array sudah penuh, kita tidak bisa melakukan itu karena array menyimpan memory yang sudah dipesan sehingga kita tidak dapat menambah kapasitas.  Link list kebalikan dari array jadi walau tidak bisa reserve memory dari awal dengan link list kita dapat menambah terus jika perlu.

Stack Operation terdapat 3 operasi pada stack yaitu:

• Push(x): Menaruh elemen x diatas stack
• Pop(): Menghilangkan elemen stack teratas
• Top(): Mengambil data teratas stack

Infix, Prefix, dan Postfix

Secara simple:

• Infix: Operasi matematika seperti biasa
• Prefix: Operasi dimana operator ditulis terlebih dahulu sebelum operand
• Postfix: Operasi dimana operand ditulis setelah operand

Contoh: 4+6*(5-2)/3 ubahlah ke bentuk postfix dan prefix!

• Postfix: 4 6 5 2 - * 3/3
• Prefix: + 4 * 6 - 5 2/3

Queue

Queue atau antiran adalah data struktur yang mirip dengan stack bedanya jika stack adalah LIFO, queue adalah FIFO (First in First Out).  Ide dari konsep queue ini sama seperti antrian di dunia nyata yaitu "One does not simply add a new person in front of a line after the former first in line is done"

Queue operation ada 3 yaitu:

• Push(x): Menaruh elemen x diakhir queue
• Pop(): Menghilangkan elemen terdepan queue
• Front(): Mengambil data terdepan queue

Hashing

A technique used for storing and retrieving keys in a rapid manner.  What hashing do basically, they are transforming a string of characters into a shorter length value or key that represents the original string and then these transform string of character is used to index and retrieve in a database since it is faster to find item using the shorter key that was previously transform.  Hashing can be defined as a concept of distributing keys in an array called hash table (which is going to be explained next) using a predetermined function called hash function.

Hash Table

A table of array in which where we store the original string.  The index of the table is the hashed key while the value is the original string.  The size of hash table is usually significantly lower than the number of possible string, so several string might have a same hashed-key.

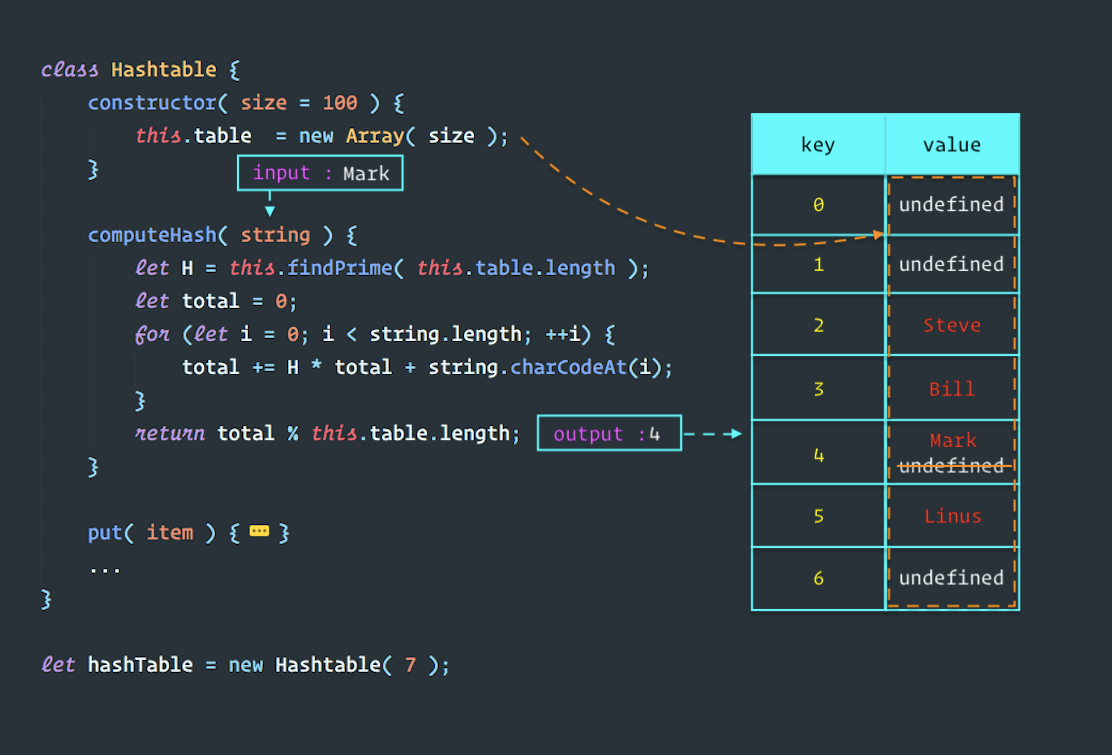1.1 Hash Table coding example.

There are many ways to hash a string and here is a few hash function to name:

• Mid-square
• Division
• Folding
• Digit Extraction
• Rotating Hash

Binary Tree

First thing first a tree is a non-linear data structure that represent the hierarchical relationships among the data object.  The data or node in the tree need not to be stored continuously and can be stored anywhere and linked by pointers.  A binary tree is a data structure in which each node has at most two children that is usually distinguished as left child and right child.

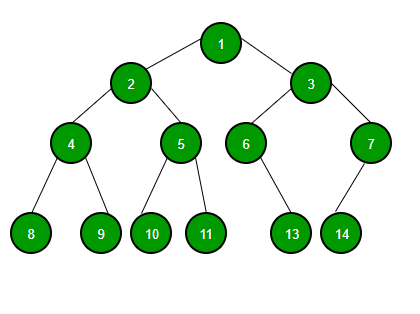1.2 Example of Binary Tree

Binary Search Tree

What is Binary Search Tree? Binary Search Tree or BST for short is a data structure that supports faster search, rapid sort, as well as easy insert and delete.  This data structure is also known as the sorted version of the Binary Tree.  In BST a node can be classified as either a left sub tree which contains the smaller element and a right sub tree which is the opposite of the left sub tree, assuming of course that each key are distinct.

A few operation in BST:

• find(x)      : Find key x in the BST
• insert(x)   : Insert new key x into BST
• remove(x): Remove key x from BST

Operation: Search

Thanks to BST property of already being sorted, finding/searching in BST is easy and fast.

For example say that we want to search for an element which is X.  First we begin from the root or the top of the tree.  If X is found within the root then the search is a success and then the programs end.  If X is less than the root's key then the search will go down onto the left sub tree, otherwise it will go down onto the right sub tree.

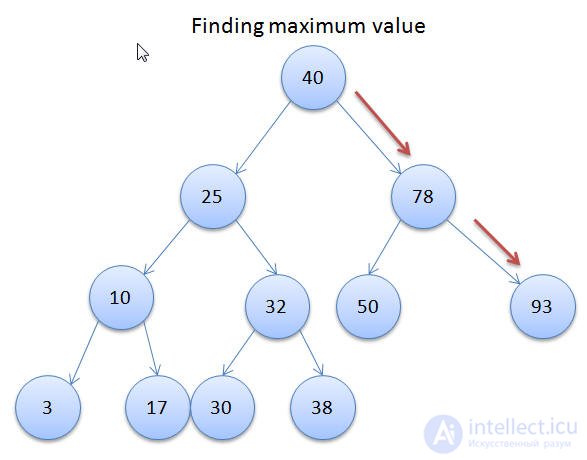
For example let's say we want to search for the number 93.  First we start at the root which is 40.  Since 40 is not the number we search, we continue our search and since 93 is bigger than 40 we delve deeper into the right sub tree.  Next we are at the position of 78 and since 93 is bigger than 78 we dive even deeper into the right sub tree and then viola we find 93.

Operation: Insert

In order to insert an element into the BST we insert it recursively.  First we begin at the root and then if X, the element we want to add, is less than the root, we go into the left sub tree, but if otherwise then we go into the the right sub tree.  This process repeat until we found an empty node to put X. Let's say for example we want to insert the element 16 on a BST.

Operation: Delete

To do deletion first we find the node first and then we need to consider 3 possible cases.

• The first if the key is in a leaf in which we just go ahead and delete that node.
• The second if the key is in a node which has one child, delete the node and then connect its child to its parent.
• The third is if the key is in a node which has two children, find the right most child of its left sub tree (node P), replace its key with P’s key and remove P recursively. (or alternately you can choose the left most child of its right sub tree)