Binary Search Tree
Binary Search Tree
What is Binary Search Tree? Binary Search Tree or BST for short is a data structure that supports faster search, rapid sort, as well as easy insert and delete. This data structure is also known as the sorted version of the Binary Tree. In BST a node can be classified as either a left sub tree which contains the smaller element and a right sub tree which is the opposite of the left sub tree, assuming of course that each key are distinct.
A few operation in BST:
- find(x) : Find key x in the BST
- insert(x) : Insert new key x into BST
- remove(x): Remove key x from BST
Operation: Search
Thanks to BST property of already being sorted, finding/searching in BST is easy and fast.
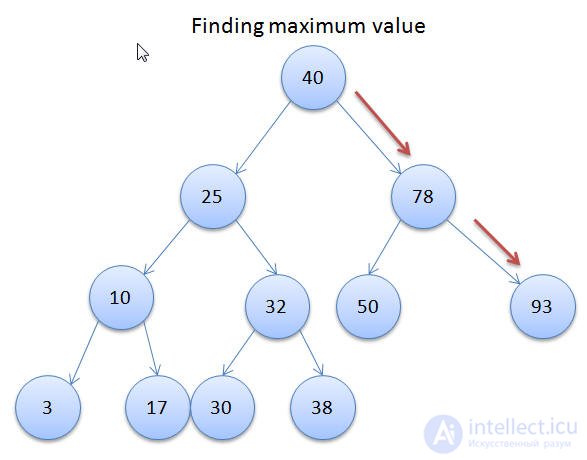
For example say that we want to search for an element which is X. First we begin from the root or the top of the tree. If X is found within the root then the search is a success and then the programs end. If X is less than the root's key then the search will go down onto the left sub tree, otherwise it will go down onto the right sub tree.
For example let's say we want to search for the number 93. First we start at the root which is 40. Since 40 is not the number we search, we continue our search and since 93 is bigger than 40 we delve deeper into the right sub tree. Next we are at the position of 78 and since 93 is bigger than 78 we dive even deeper into the right sub tree and then viola we find 93.
Operation: Insert
In order to insert an element into the BST we insert it recursively. First we begin at the root and then if X, the element we want to add, is less than the root, we go into the left sub tree, but if otherwise then we go into the the right sub tree. This process repeat until we found an empty node to put X. Let's say for example we want to insert the element 16 on a BST.
Operation: Delete
To do deletion first we find the node first and then we need to consider 3 possible cases.
- The first if the key is in a leaf in which we just go ahead and delete that node.
- The second if the key is in a node which has one child, delete the node and then connect its child to its parent.
- The third is if the
key is in a node which has two children, find the right most child of its left
sub tree (node P), replace its key with P’s key and remove P recursively. (or
alternately you can choose the left most child of its right sub tree)